
 |
Basic Maths for Protein Crystallographers |
| Intensity statistics |
|
|
A good deal can be inferred from the intensity statistics and relationships between them. Certainly they are an excellent way of assessing the quality of our experiment.
I(h) = F(h) F(h)* = |F(h)|2
The mean value of <F(h) F(h)*> (S) =
![]() g(j,S)2
g(j,S)2
since the average of the second summation wil be zero.
If all atoms have the same temperature factor, i.e.
g(j,S) = f(i,S)e-2Bs²
then
<F(h)F(h)*> (S) = e-2Bs²f(j,S)2
Our measured I(h) will be on an arbitrary scale so we expect
and after dividing both sides by ![]() and taking logs:
and taking logs:
log k = log{<Iobs(h)>/} = -2B s²
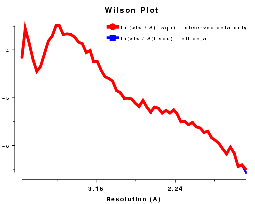
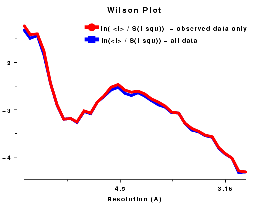
The Wilson Plot is simply the plot of
log{<Iobs(h)>/![]() }
and should be a straight line with gradient -2B. For proteins the low resolution data
does not usually generate such a straight line. In fact the atoms are not distributed randomly within the
crystal and the solvent regions are much less well-ordered than the protein. This generates a
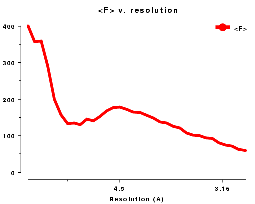
distribution of <Iobs(h)> of the type shown in Figures WL and WR.
For data below 10Å <Iobs(h)> is large, but it
dips at about 5Å. From about 4Å on the solvent contribution to
the structure amplitude is very small, and we get a reasonably straight line corresponding to
the scattering from the ordered atoms.
}
and should be a straight line with gradient -2B. For proteins the low resolution data
does not usually generate such a straight line. In fact the atoms are not distributed randomly within the
crystal and the solvent regions are much less well-ordered than the protein. This generates a
distribution of <Iobs(h)> of the type shown in Figures WL and WR.
For data below 10Å <Iobs(h)> is large, but it
dips at about 5Å. From about 4Å on the solvent contribution to
the structure amplitude is very small, and we get a reasonably straight line corresponding to
the scattering from the ordered atoms.
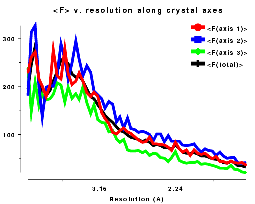
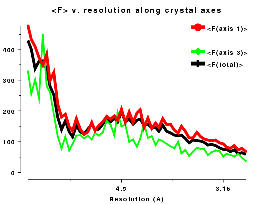
Plots on the left are for a data set in P212121 with translational NCS, plots on the right from a partially twinned data set in R3. These pictures each hide a larger (better resolution) picture, which will appear in a separate window upon clicking the small version.
|
|
| Figure WL | Figure WR |
|
|
| Figure AL | Figure AR |
|
|
| Figure FL | Figure FR |
Normalised intensities and amplitudes are generated by modifying I(h) to give Z(h)
and then defining E(h) as equal to sqrt(Z(h)).
The definition is that <Z(S)> = 1 for all resolution shells (S is
defined as (d*)2, or
![]() ),
i.e. every intensity, I(h), is
divided by <I(S)> for that resolution range.
),
i.e. every intensity, I(h), is
divided by <I(S)> for that resolution range.
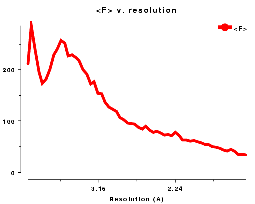
In other words, the normalised structure intensity for a reflection, Z(h), is taken as the structure intensity divided by the product of the r.m.s. value of the structure intensities in the appropriate resolution shell corrected for the epsilon factor which is dependent on the Laue group symmetry. This takes account of the fact that for macromolecular structures the low resolution <I> distribution is very different from the Wilson ideal. Ref Figure of <I(S)> v resolution..
This approach was suggested by Karle; small molecule crystallographers often normalise their data by applying an overall temperature factor obtained from a Wilson plot ( Ref???).
The normalisation method is also described in the ECALC documentation:
Since E(h) is defined as equal to sqrt(Z(h)), it can also be written as sqrt(I(h)/<I(S)>); and <E2> = 1.
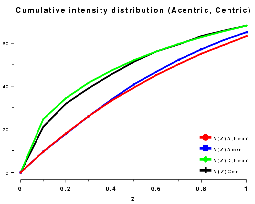
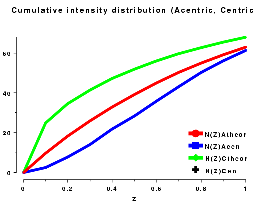
The cumulative intensity distribution plots the percentage of acentric and centric reflections where (Z(h) is less than 0.1, 0.2, up to 1.0. For a crystal with more or less randomly distributed atoms this follows a predictable distribution, as can be seen by plotting the output of TRUNCATE or ECALC (see also Figure CL below). The distribution can be misleading if the data is of poor quality, or there is strong translational non-crystallographic symmetry, which may cause whole classes of reflections to be virtually unobserved.
For a twinned crystal where in fact each observed "I(h)" is the sum of two or more overlapping reflections, the distribution becomes rather sigmoidal; since it is unlikely that both contributions to I(h) will be weak, it appears that there are fewer weak intensities than expected (see Figure CR below).
Plots on the left are for a data set in P212121 with translational NCS, plots on the right from a partially twinned data set in R3. These pictures each hide a larger (better resolution) picture, which will appear in a separate window upon clicking the small version.
|
|
| Figure CL | Figure CR |
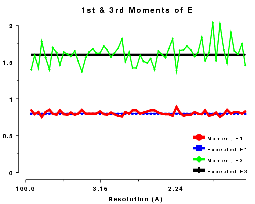
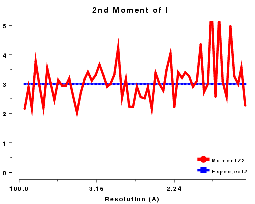
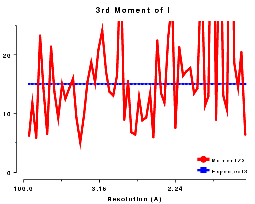
The moments of the data provide some of the most sensitive tests for both data quality and twinning. If these deviate in certain ways you probably have measured twinned data. If they fluctuate you may have made a mess of processing.
The definition of the k-th moment of a variable x is:
<xk> / <x>k where < > denotes the mean value
So the k-th moment of I is
<Ik> / <I>k
And the k-th moment of E, defined as
<Ek> / <E>k
is equal to the (k/2)-th moment of I.
The structure factor formula (ref.[1]) means that the expected values for these moments can be calculated when k is a simple power, e.g. ½, 1, 2, 3, ...
Using the structure factor formula it can be shown that the k-th moment of E is
![]() (k/2 + 1)
(k/2 + 1)
The ![]() -function is defined by the
recursive relationship
-function is defined by the
recursive relationship
![]() (x + 1) =
x
(x + 1) =
x ![]() (x)
(x)
We are only interested in small, positive integer moments. It can be shown that
![]() (n + 1) = (n)!
(n + 1) = (n)!
And also
![]() (n + 1/2) =
[sqrt(
(n + 1/2) =
[sqrt(![]() )/2n] * (2n-1) * (2n-3) * ...* 1
)/2n] * (2n-1) * (2n-3) * ...* 1
So, for example
With all that in mind, the moments of E are:
| for acentric data: |
|---|
= (k/2)! if k is even = sqrt( |
| for centric data: |
[2(k/2)/sqrt(= [2(k/2)/sqrt( = (k-1) * (k-3) * ... * 1 if k is even |
XXX The values for perfectly twinned data can also be derived mathematically. Ref XXX
Some numerical examples:
| Acentric | Centric | |||
|---|---|---|---|---|
| Untwinned data | Perfect twin | Untwinned data | Perfect twin | |
| <E> | 0.886 | 0.94 | 0.798 | ? |
| <E3> | 1.329 | 1.175 | 1.596 | ? |
| <I2> | 2.0 | 1.5 | 3.0 | ? |
| <I3> | 6.0 | 3.0 | 15.0 | ? |
| <I4> | 24.0 | 7.5 | 105.0 | ? |
Plots on the left are for a data set in P212121 with translational NCS, plots on the right from a partially twinned data set in R3. These pictures each hide a larger (better resolution) picture, which will appear in a separate window upon clicking the small version.
Plots below are from a data set in P212121 with translational NCS. These pictures each hide a larger (better resolution) picture, which will appear in a separate window upon clicking the small version.
|
1st and 3rd moments of E, centric data, P212121 |
|
2nd moment of I or z or E2, centric data, P212121 |
|
3rd moment of I or z, centric data, P212121 |